
강화학습 쉽지 않습니다. 그런데 정말 재미있는 분야인 것 같습니다. 이번 글을 통해 강화학습의 기본 Q-Learning을 설명드리겠습니다.
강화학습 (Reinforcement Learning)
강화학습은 기계 학습의 한 종류로 어떤 환경(env) 안에서 정의된 에이전트(agent)가 현재의 상태(state)를 인식하여, 선택 가능한 행동(action)들 중 보상(reward)을 최대화하는 행동 혹은 행동 순서를 선택하도록 학습시키는 방법입니다.

그렇다면 강화학습을 구현하기 위한 방법에는 무엇이 있을까요? 대표적으로 Q-Learning과 DQN(Deep Q Network)가 있습니다. 우리는 여기서 Q-Learning이 구체적으로 무엇인지 배우고 러프하게 코드를 구현해보겠습니다.
Q-Learning 이론 : Q-table
Q-Learning은 Q 함수를 통해 Q-table을 최적의 Q-table로 업데이트 하는 방법입니다. Q-table은 agent가 선택할 수 있는 action과 state에 대한 조합으로 구성됩니다.
학습을 시작하는 처음, Q-table 내부의 값은 모두 무작위로 초기화되어 있습니다. 그러나 학습을 반복할 수록 agent는 action을 통해 받은 reward 및 Q 함수 계산을 통해 reward를 가장 많이 받을 수 있는 action-state 조합에 가장 높은 가치를 저장하게 됩니다. (추후 언급할 epsilon-greedy 정책에 따라서요)
이 때 주의해야 할 점은 아래 그림은 Q-table 내 action-state의 상관관계를 보여주기 위해 시각적으로 단순화한 것이지 실제 코드에서 Q-table은 단순한 2차원 배열로 구성되는 것이 아님을 명심하세요. 훨씬 더 복잡합니다.

Q-Learning 이론 : Q 함수
앞서 말씀드린 Q-table을 계속 최적의 Q-table로 업데이트하도록 계산하는 함수가 Q 함수입니다. Q 함수는 다음과 같이 구성됩니다. 엔지니어는 learning rate, reward, discount factor 값을 조정하여 각 상황에 가장 적합한 Q 함수를 설계할 필요가 있습니다.

Q-Learning 코드 구현
러프하게 Q-Learning 코드를 구현해 보겠습니다. 비트코인 자동 매매봇을 만들어 본다고 가정합니다.
Q-table을 구현하기 위해 numpy 라이브러리를 사용하겠습니다.
import numpy as np
Q-table 생성 함수와 State 값을 이산화하는 함수를 구현합니다. 저는 State로 이전 시세 증감 값과 거래량 두 개로 설정하겠습니다.
# Q 테이블 생성
# bins = [이전 시세 증감, 거래량]
def Qtable(state_space,action_space,bin_size = 30):
bins = [np.linspace(-4,4,bin_size),
np.linspace(-4,4,bin_size)]
q_table = np.random.uniform(low=-1,high=1,size=([bin_size] * state_space + [action_space]))
return q_table, bins
# 이산화 함수
# Q 테이블이 지나치게 방대해 지는 것을 막기 위해 단순화 작업이 반드시 필요합니다.
def Discrete(state, bins):
index = []
for i in range(len(state)): index.append(np.digitize(state[i],bins[i]) - 1)
return tuple(index)
# 이산화 작업 예
# print(Discrete((-58000, 4.11099952), bins)) ---> -1, 12
Q-Learning 함수를 설계합니다. epsilon-greedy 정책을 반영하려면 원하는 epsilon-greedy 정책 코드를 집어넣어 주세요, 아래 코드에는 epsilon이 항상 일정합니다. (효율적인 epsilon-greedy 정책이 반영되지 않아 좋은 학습 결과를 도출하지 않음)
epsilon-greedy 정책은 공식이 있는 것이 아닙니다. 상황에 맞게 적절한 epsilon-greedy 정책을 각자 설정하여 작용해야 합니다. (예: episode 100번째 마다 epilson -= (epsilon * episode) / episodes)
def Q_learning(q_table, bins, episodes = 5000, gamma = 0.95, lr = 0.1, timestep = 5000, epsilon = 0.2):
rewards = 0
data = {'score' : [0]}
# 에피소드 갯수만큼 학습을 반복
for episode in range(1,episodes+1):
# 초기 값을 넣는다. (5월 13일 17시 21일 state)
current_state = Discrete([-58000, 4.11099952],bins) # initial observation
score = 0
# 0 : 중립, 1 : 매수, 2 : 매도
done = False # 미사용
temp_start = time.time()
# 학습 데이터를 처음부터 끝까지 학습
for index, next_stock in enumerate(train_data):
if not done:
# 액션 선택
# 엡실론-그리디 정책에 따라, 어느 정도 확률로 무작위 액션을 시행
if np.random.uniform(0,1) < epsilon:
action = random.choice([0, 1, 2])
else:
# 또는 최적의 Q-value에 따른 액션을 선택
action = np.argmax(q_table[current_state])
# 현재 인덱스에 해당하는 주가 데이터를 보고 해당 선택에 대한 리워드를 지급
# 매수 행동
if action == 1:
# 리워드 매수 행동에 맞게 지급
# 매도 행동 (차익)
elif action == 2:
# 리워드 매도 행동에 맞게 지급
# 중립 행동
else:
# 리워드 중립 행동에 맞게 지급
# 상태 설정
next_state = Discrete([next_stock['tradePrice'] - current_stock['tradePrice'], next_stock['candleAccTradeVolume']], bins)
score += reward
# 받은 reward를 감안한 Q value 업데이트
max_future_q = np.max(q_table[next_state])
current_q = q_table[current_state+(action,)]
new_q = (1-lr)*current_q + lr*(reward + gamma*max_future_q)
q_table[current_state+(action,)] = new_q
# 일반적으로 여기에 epsilon-greedy 정책을 설계합니다.
if episode%100 == 0 and epsilon > 0.001:
epsilon -= (epsilon * episode)/episodes
이제 Q-table 생성 및 Q-learning 함수를 실행합니다.
# TRANING
q_table, bins = Qtable(2, 3)
Q_learning(q_table, bins, lr = 0.15, gamma = 0.995, episodes = 5*10**3, timestep = 1000)학습 후 학습 결과를 시각화하여 의도한 대로 학습되었는 지 확인해 보세요. 의도에 맞지 않게 학습되었을 경우 학습 데이터셋, 이산화 방법, lr(Learning Rate), gamma(Discount Factor), action에 대한 reward 지급 방법, epsilon-greedy 정책을 수정해 보세요. 경험 상 학습 데이터셋 갯수와 epsilon-greedy 정책 수정에 집중하는 걸 추천드립니다.
Q-Learning과 DQN(Deep Q Network)
Q-Learning은 Q-table 이라는 자료 구조 속에 최적의 행동 조합을 업데이트합니다. DQN은 Q-table이 아인 Neural Network 에 최적의 행동 조합을 업데이트합니다. 참고로 Q-Learning 보단 DQN 성능이 월등하다고 하네요.
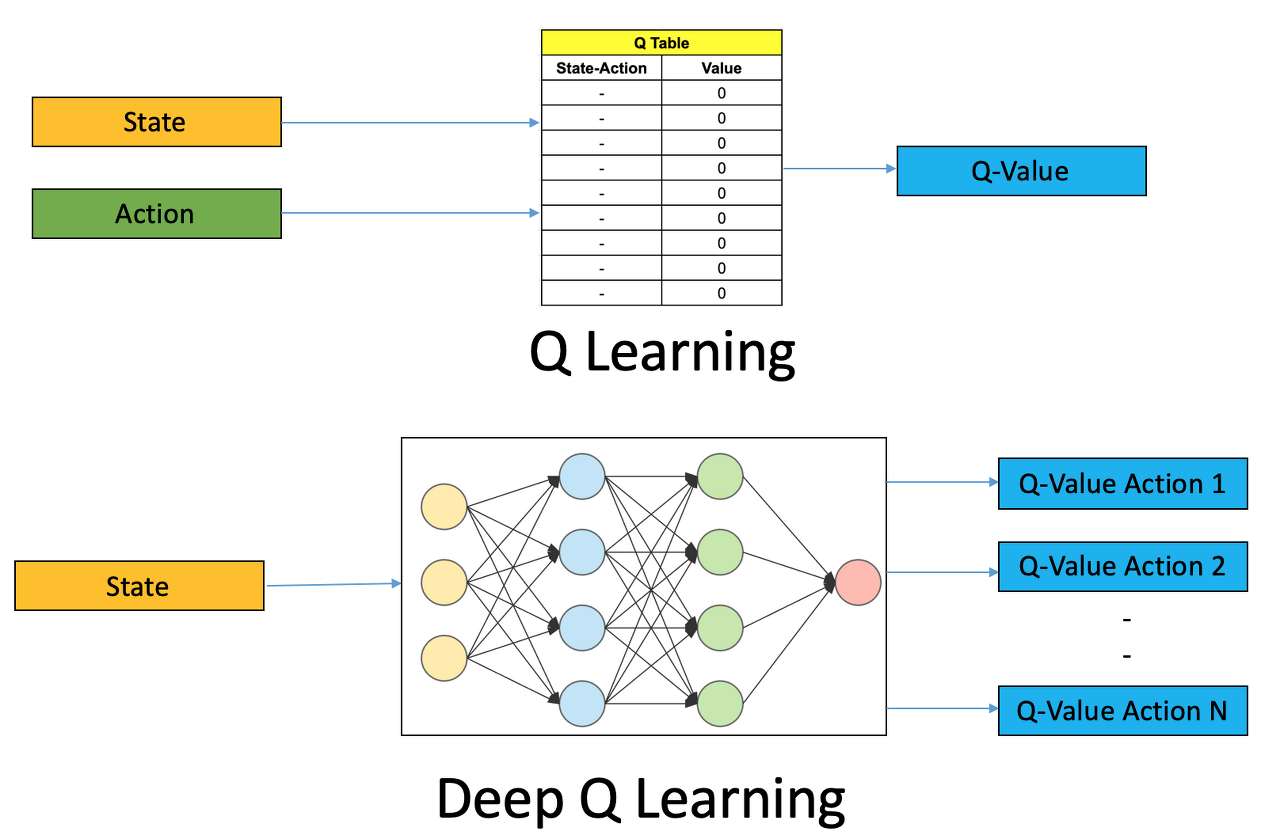
출처
Q-Learning is the most basic form of Reinforcement Learning, which doesn’t take advantage of any…
Background information
medium.com
Q 러닝 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. Q 러닝(Q-learning)은 모델 없이 학습하는 강화 학습 기법 가운데 하나이다. Q 러닝은 주어진 유한 마르코프 결정 과정의 최적의 정책을 찾기 위해 사용할 수 있다.
ko.wikipedia.org
GitHub - maciejbalawejder/Reinforcement-Learning-Collection
Contribute to maciejbalawejder/Reinforcement-Learning-Collection development by creating an account on GitHub.
github.com
'컴퓨터공학 & 정보통신' 카테고리의 다른 글
| [컴퓨터그래픽스] Parametric Surface, Homogeneous Coordinate, Raytracing (0) | 2023.06.12 |
|---|---|
| [컴퓨터그래픽스] polygonal mesh, subdivision, Mesh Data Structure (0) | 2023.06.12 |
| [자료구조] Planar graph 와 plane graph (0) | 2023.05.31 |
| [컴퓨터그래픽스] Winged edge table (0) | 2023.05.29 |
| [머신러닝] Linear Regression (0) | 2023.04.25 |



